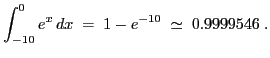
sparse) que nous n'aborderons pas.
Il est important de garder à l'esprit que tous les calculs numériques dépendent de la représentation des nombres réels en machine, et que donc les résultats ``exacts'' n'existent pas. La détection de singularités dépend d'une précision prédéfinie et n'est donc pas infaillible.
rank([1,1;1,1]) rank([1.00000000000001,1;1,1]) rank([1.000000000000001,1;1,1]) inv([1,1;1,1]) A=[1,2,3;4,5,6;7,8,9] det(A) det(A') rank(A) inv(A) // le calcul est effectue inv(A') // message d'erreur A*inv(A) // ce n'est pas l'identite
Si A et B sont deux matrices, alors A\B retourne
une matrice X telle que A*X=B, et B/A une matrice
X telle que X*A=B pourvu que les dimensions
de A et B soient compatibles. Si A n'est pas une
matrice carrée inversible, ces commandes retourneront un résultat,
qu'il y ait une infinité de solutions ou qu'il y en ait aucune.
A=[1,2,3;4,5,6;7,8,9] b=[1;1;1] x=A\b // le systeme a une infinite de solutions A*x b=[1,1,1] x=b/A // le systeme a une infinite de solutions x*A b=[1;1;2] x=A\b // le systeme n'a pas de solution A*x b=[1,1,2] x=b/A // le systeme n'a pas de solution x*A
Si A est carrée et régulière x=A\b est unique et
équivalent mathématiquement à x=inv(A)*b mais plus rapide.
b=[1:500]'; A=diag(b); timer(); A\b ; timer() timer(); inv(A)*b ; timer()
Pour résoudre un système linéaire quand on craint une
singularité, il vaut mieux utiliser linsolve, qui détecte
les impossibilités et peut retourner une base du noyau de la matrice
en cas de solutions multiples. Attention, linsolve(A,b) résout
A*x=-b.
A=[1,2,3;4,5,6;7,8,9] b=[1;1;1] [x,k]=linsolve(A,b) A*x A*k b=[1;1;2] [x,k]=linsolve(A,b) // erreur
La commande [D,U]=bdiag(A) retourne (en théorie) une matrice diagonale
D et une matrice inversible U telles que
U*D*inv(U)=A.
A=diag([1,2,3]); P=rand(3,3); A=P*A*inv(P) spec(A) [D,U]=bdiag(A) // matrice diagonalisable inv(U)*A*U U*D*inv(U)-A A=[1,0,0;0,1,1;0,0,1]; P=rand(3,3); A=P*A*inv(P) spec(A) [D,U]=bdiag(A) // matrice non diagonalisable inv(U)*A*U U*D*inv(U)-A [X,diagevals]=spec(A)
La décomposition LU d'une matrice, c-à-d la décomposition
en produit d'une matrice triangulaire inférieure L et d'une matrice triangulaire supérieure U,
à des permutations près,
s'obtient grâce à la commande lu.
A= [ 1, 2, 3; 4, 5, 6 ; 7, 8, 9 ] [L,U,E]=lu(A) E*A-L*U det(U) det(A)
| Opérations matricielles | |
A' |
transposée de A |
rank |
rang |
lu |
décomposition LU |
inv |
inverse |
expm |
exponentielle matricielle |
det |
déterminant |
trace |
trace |
poly(A,"x") |
polynôme caractéristique de A |
spec |
valeurs propres de A |
bdiag |
diagonalisation |
svd |
décomposition en valeurs singulières |
A\b |
solution de A*x = b |
b/A |
solution de x*A = b |
linsolve(A,b) |
solution de A*x = -b |
integrate, intg,
int2d, int3d, intc et intl prennent
en entrée une fonction externe, ou définie par une chaîne
de caractères. Les fonctions inttrap et
intsplin prennent en entrée des vecteurs d'abscisses et
d'ordonnées.
| Calculs d'intégrales | |
integrate |
fonction définie par une chaîne de caractères |
intg |
fonction externe |
inttrap |
méthode des trapèzes |
intsplin |
approximation par splines |
int2d |
fonction de deux variables |
int3d |
fonction de trois variables |
intc |
fonction complexe le long d'un segment |
intl |
fonction complexe le long d'un arc de cercle |
Dans l'exemple ci-dessous, on calcule avec les différentes fonctions d'intégration disponibles, la valeur de :
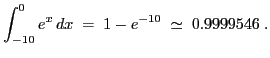
x = [-10:0.1:0];
y=exp(x);
1-1/%e^10
inttrap(x,y)
intsplin(x,y)
integrate("exp(x)","x",-10,0)
deff("y=f(x)","y=exp(x)")
intg(-10,0,f)
Les algorithmes de calcul numérique des transformées classiques
sont disponibles. Le tableau ci-dessous en donne quelques-unes, voir
apropos transform pour les autres.
| Transformées | |
dft |
transformée de Fourier discrète |
fft |
transformée de Fourier rapide |
convol |
produit de convolution |
fsolve résout numériquement un système d'équations,
mis sous la forme
deff("y=f(x)","y=sin(%pi*x)")
fsolve(0.2,f)
fsolve(0.4,f)
fsolve(0.45,f)
fsolve(0.5,f)
fsolve([0.45:0.01:0.5],f)
help fsolve
[x,v,info]=fsolve(0.5,f)
[x,v,info]=fsolve([0.45:0.01:0.5],f)
| Résolutions | |
fsolve |
systèmes d'équations |
roots |
racines d'un polynôme |
factors |
facteurs irréductibles réels d'un polynôme |
linsolve |
systèmes linéaires |
La fonction optim recherche un minimum (local) d'une fonction dont on
connaît le gradient. La définition de la fonction en entrée est un peu
particulière. Le choix de trois algorithmes
différents est offert en option.
help optim
deff("[y,yprim,ind]=f(x,ind)","y=sin(%pi*x),yprim=%pi*cos(%pi*x)")
[x,v]=optim(f,0.2)
[v,xopt]=optim(f,0.50000000000000001)
[v,xopt]=optim(f,0.5000000000000001)
| Optimisation | |
optim |
optimisation |
linpro |
programmation linéaire |
quapro |
programmation quadratique |
ode est en fait un environnement qui donne
accès à la plupart des méthodes numériques classiques
pour la résolution des équations différentielles ordinaires
(voir help ode).
A titre d'exemple nous commençons par le problème de Cauchy en dimension 1 suivant :
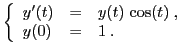 |
La solution explicite est
![]() . La résolution numérique
par
. La résolution numérique
par ode est très stable.
deff("yprim=f(t,y)","yprim=y*cos(t)")
t0=0; y0=1; t=[0:0.01:10];
sol=ode(y0,t0,t,f);
max(abs(sol-exp(sin(t)))) // l'erreur est tres faible
t0=0; y0=1; t=[0:0.1:100];
sol=ode(y0,t0,t,f);
max(abs(sol-exp(sin(t)))) // l'erreur reste tres faible
La situation n'est pas toujours aussi favorable.
Considérons par exemple
![]() , solution du problème de
Cauchy suivant.
, solution du problème de
Cauchy suivant.
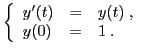 |
deff("yprim=f(t,y)","yprim=y")
t0=0; y0=1; t=[0:0.01:10];
sol=ode(y0,t0,t,f);
max(abs(sol-exp(t))) // l'erreur est raisonnable
t0=0; y0=1; t=[0:0.1:100];
sol=ode(y0,t0,t,f);
max(abs(sol-exp(t))) // l'erreur est enorme
Voici en dimension 2 la résolution d'un système différentiel de Lotka-Volterra, avec superposition de la trajectoire calculée et du champ de vecteurs défini par le système (figure 8).
//
// definition du systeme
//
deff("yprim=f(t,y)",..
["yprim1=y(1)-y(1)*y(2)";..
"yprim2=-2*y(2)+2*y(1)*y(2)";..
"yprim=[yprim1;yprim2]"])
//
// champ de vecteurs
//
xmin=0; xmax=3; ymin=0; ymax=3;
fx=xmin:0.3:xmax; fy=ymin:0.3:ymax;
clf()
fchamp(f,1,fx,fy)
//
//resolution du systeme
//
t0=0; tmax=5; pas=0.1
t=t0:pas:tmax;
y0=[2;2];
sol=ode(y0,t0,t,f);
//
// trace de la trajectoire
//
plot2d(sol(1,:),sol(2,:),5,"000")
![\includegraphics[width=10cm]{lotka.eps}](img59.png)
|